AVL트리에 대략적으로 기억하고 문제를 본다면 다소 헷갈릴수 있는 부분이 있다.
첫째, 어떻게 계산을 하는걸까?
둘째, 데이터의 삽입 또는 삭제로 균형이 깨지는 경우, 회전연산을 이용하는데 어떤것을 기준으로 하는걸까?
셋째, 만약 균형이 깨진 곳이 두군데라면 어느곳을 바꿔야 하는걸까?
넷째, 회전 연산의 종류는 LL,LR,RR,RL 회전이 있는데 회전의 기준은 어떻게 되는 것일까?
다섯째, 회전 연산의 이름은 어떻게 붙여진 것일까?
여섯째, 삽입하는 경우 어느 위치로 배정되는 것일까?
위의 문제를 차근차근 해결할수 있다면 AVL트리를 온전히 이해한 것이라 볼 수 있을것이라 생각한다. (공부하면서 궁금했던 부분들이었다.)
맨 처음에는 'Mar'이라는 데이터가 들어왔다.

'Mar' 위에 0이라는 숫자가 보이는데, 좌우 서브트리의 깊이(level)의 차이가 0인 것을 의미한다.
좌우 서브트리의 깊이(level)이라는 것은 데이터를 몇개만 더 삽입해본다면 알 수 있다.

이번에는 'May'라는 데이터가 들어왔다. 이때, Mar과 May를 정렬하고 데이터를 저장한다.
Mar과 May의 차이는 '스펠링' 'r'과 'y'라는 것. 따라서 Mar 다음 순서로 May가 오게 된다.
데이터가 큰 쪽의 노드는 데이터가 작은 쪽의 노드의 우측 하단에 배치를 하게된다.
이와는 반대로 데이터가 작은 쪽의 노드는 데이터가 큰 쪽의 노드의 좌측 하단에 배치를 하게된다.

'Mar'과 'May'에서 'M'과'a'는 동일하기 때문에 비교할수 없다. 하지만, 'y'가 'r'보다 크기 때문에 'May'는 'Mar'의 우측 하단에 배치된다.
그리고 여기서 노드 위에, 해당 노드의 서브트리의 깊이(level)를 계산한 결과를 적어줘야 한다.
다음으로 넘어가기 전에 결과가 어떻게 될지 생각해보셨으면 좋겠다.
덧붙여서,
계산을 할 때는, 순서가 중요하다.
좌측 서브트리의 깊이(level)에서 우측 서브트리의 깊이(level)의 차를 구해야 한다.
계산한 결과는 다음과 같다.

이유를 설명하자면,
Mar의 좌측 서브트리의 level은 좌측 서브트리가 없기 때문에 '0'이고, 우측 서브트리의 level은 May노드 한 개이기 때문에 1이다. 따라서, 0 - 1 = -1 이기 때문에 Mar의 결과는 -1이고,
May는 좌/우측의 서브트리가 없기 때문에 0 - 0 = 0이므로 May의 결과는 0이 된다.
다음은, 'Nov'데이터를 가진 노드가 들어왔다.
그러면 'Nov'데이터의 정렬만 해보면, 'Nov'는 어느 위치에 배치하면 되는걸까?

'Nov'의 'N'은 'Mar'의 'M'보다 큰 값이고, 마찬가지로 'May'의 'M'보다 큰 값이다.
따라서 'Nov'는 'May'의 우측 하단에 배치한다.
그리고 각 노드 위에 서브트리의 차를 구한 값을 적어준다.

AVL 서브트리는 균형 탐색 트리이기 때문에, 좌우 서브트리의 깊이의 균형을 지속적으로 유지하는 것을 목표로 한다.
따라서, 위와 같은 경우처럼 좌우 서브트리의 깊이(level)의 차이가 2 이상이 된다면, 차이가 2 이상이 되지 않게 트리의 모양을 재구성해야 한다.
여기서 Mar < May < Nov 순서이기 때문에 트리의 균형을 맞춰주기 위해서는 위에서 언급한 것처럼
데이터가 큰 쪽의 노드는 데이터가 작은 쪽의 노드의 우측 하단에 배치한다.
이와는 반대로 데이터가 작은 쪽의 노드는 데이터가 큰 쪽의 노드의 좌측 하단에 배치한다.
이것을 떠올려 본다.
그 결과 트리를 재배치 해본다면, 다음과 같은 트리의 모양을 만들 수 있다.

여기서 각 노드 위에 좌우 서브트리의 깊이(level)의 차를 계산한 결과를 적는다면 아래와 같다.

May노드 : 1 - 1 = 0
Mar노드 : 0 - 0 = 0
Nov노드 : 0 - 0 = 0
이때, 'Aug'데이터를 가진 노드가 들어왔다면 트리구조와 계산 결과는 어떻게 될까?
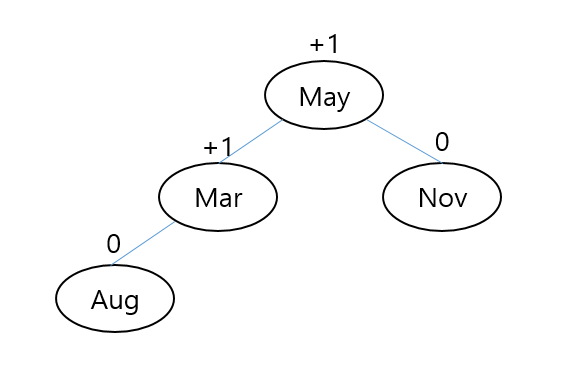
계산 과정은 다음과 같다.
May노드 : 2 - 1 = 1
Mar노드 : 1 - 0 = 1
Nov노드 : 0 - 0 = 0
Aug노드 : 0 - 0 = 0
'Aug'의 'A'는 'May'와 'Mar'의 'M'보다 작기 때문에 'Mar'의 좌측 하단에 배치된다.
그리고 'Apr'데이터를 가진 노드가 들어온다면 트리가 어떻게 구성되고 계산 결과는 어떻게 되는지 만들어보자.

이 때,
좌/우 서브트리의 차이가 2 인 노드가 발견됐다.
그것도 두 개나 !

그러면 이제 고민은 '어떤 노드'를 기준으로 서브트리를 재구성할 지 생각해봐야 한다.
이때는 노드 두 개중 아래쪽에 있는 노드의 서브트리를 바꾼다.
맨 위의 'May' 노드를 바꾸는 것보다 'Mar'노드를 바꾸는 것이 노드들을 조금 덜 재배치하기 때문에, 합리적이다. 그렇기 때문에 아래쪽에 있는 노드의 서브트리를 재배치 하는것 같다.

여기서 Apr < Aug < Mar 순서이기 때문에 트리의 균형을 맞춰주기 위해서는 위에서 언급한 것처럼
데이터가 큰 쪽의 노드는 데이터가 작은 쪽의 노드의 우측 하단에 배치한다.
이와는 반대로 데이터가 작은 쪽의 노드는 데이터가 큰 쪽의 노드의 좌측 하단에 배치한다.
이 규칙대로 트리의 모양을 재구성하고 계산 결과를 적어봅시다.
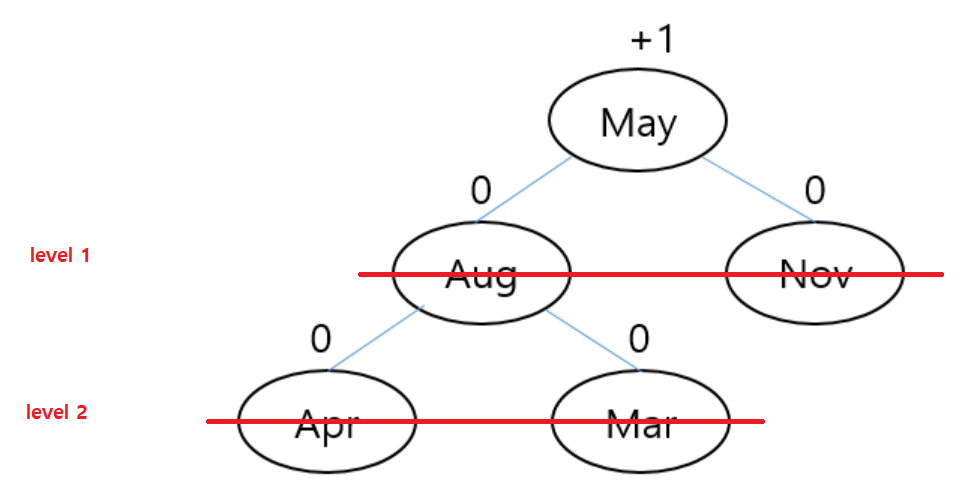

이제는 'Jan'데이터를 가진 노드가 들어왔다면,
트리를 어떻게 재구성 해야 하고, 계산 결과는 어떻게 되는지 그려봅시다.

그 결과, 좌측 서브트리의 깊이(level)와 우측 서브트리의 깊이(level) 차이가 2인 곳이 발견되었습니다.
그러면, 이제 어느 부분을 수정해야 할까요?
해당 트리를 조사할 때,
좌/우 서브트리의 차이가 2인 곳을 시작으로 해서 가장 마지막에 삽입한 노드들의 엣지(간선)를 확인합니다.
이 중에서 우리가 트리를 수정해야 할 부분은 어디일까요?

고쳐야 하는 부분의 시작 노드는 좌측 서브트리의 깊이(level)와 우측 서브트리의 깊이(level) 차이가 2인 곳,
그리고 새로 들어온 노드까지의 엣지를 따라서 시작 노드를 포함한 3개의 노드를 수정해야 합니다.

그렇다면 이제 May, Aug, Mar의 크기를 비교해봅시다.
'M'과 'A' 중 작은 것은 'A'이기 때문에 Aug가 가장 작은 데이터가 됩니다.
그리고 'May'와 'Mar'을 비교했을 때, 'Ma'는 같기 때문에 순서를 비교할 수 없습니다. 그러나 'y'와 'r'중 'y'가 알파벳 순서상 뒷쪽이기 때문에 'y'가 더 큰 데이터이므로 Mar < May 순이 됩니다.
따라서 세 노드의 크기는 Aug < Mar < May 순서가 됩니다.
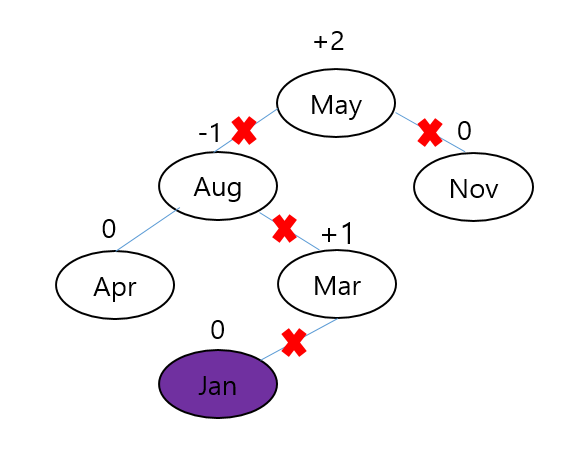

그리고 세 노드의 위치가 재배열되었기 때문에, 세 노드와 연결된 노드들이 제대로 배열이 되어있는지 확인해야 합니다.
Aug와 연결된 Apr을 보면 Aug는 아까와 같은 위치에 있기 때문에 Aug의 좌측하단에 Apr이 있는 것이 맞습니다.(그리고 알파벳 순서를 비교해봤을 때도 'Aug'의 'u'보다 'Apr'의 'p'가 더 작기 때문에 이것으로도 확인이 가능합니다.)
이 경우에서 봤듯이, 우리는 모든 링크를 확인하는 것이 아니라
링크가 끊어진 뒤, 다시 연결되어야 하는 부분들을 살펴봐야 합니다.
즉, 'May'와 'Nov'의 링크가 끊어졌고, 'Mar'과 연결되어 있던 노드인 'Jan'의 링크가 끊어졌습니다.
따라서 'Nov'와 'Jan'노드는 어디로 가야할지 생각해봐야 합니다.


노드들을 재배치 했다면, 이제 좌측과 우측의 서브트리 깊이(level)의 차를 계산해서 적어주시면 됩니다.
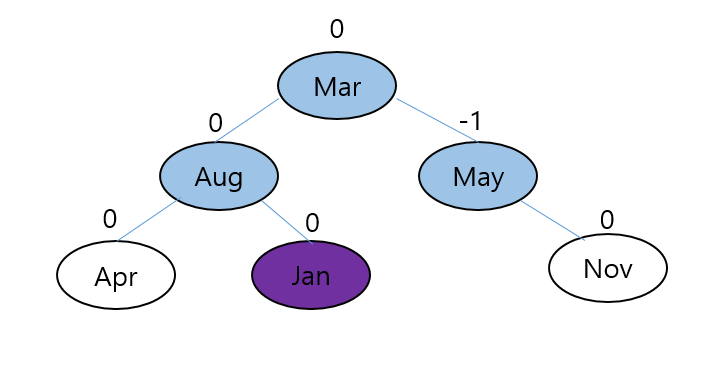
'--------------------**** > 알고리즘' 카테고리의 다른 글
| 다단계 합병에서 런의 분포 (0) | 2019.12.27 |
|---|---|
| 깊이 우선 순회 DFS - 스택 이용 (0) | 2019.12.26 |
| KMP알고리즘 코드로 이해하기 (0) | 2019.12.23 |
| KMP 알고리즘/개선된 KMP 알고리즘 & next[]의 FSM 다이어그램 (0) | 2019.12.21 |
| 알고리즘 공부했던 방법 (1) | 2019.12.14 |



