InitNext(char *p)
{
int i, j, M;
M = strlen(p);
next[0] = -1;
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
}
이번에 살펴볼 내용은 KMP알고리즘을 코드로 확인해 보는 것입니다.
패턴은 지난번과 마찬가지로 ababbaaa입니다. 따라서 M=strlen(p)에서 M은 8이 됩니다.
InitNext()를 보면, next[0]=-1이 들어가 있습니다.
그리고 for()안쪽을 확인해보면 다음과 같습니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
i와 j를 초기화 해주기 위해 i=0, j=-1을 대입하고, i가 M보다 작은지를 확인합니다.
처음에는 아래와 같은 내용으로 표를 만들어 봅니다.

그리고 for문을 다시한번 살펴봅니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
i=0, j=-1을 해준 뒤, i<M인 범위안에 들어갔으니 while()의 조건을 봐야 합니다.
while(j >= 0 && p[i] != p[j])
하지만 여기서 j=-1이기 때문에 j>=0인 조건이 성립하지 않습니다.
따라서 while 안쪽 j = next[j];를 해주지 않고,
i++, j++, next[i]=j를 해주게 됩니다.
이 부분을 공부하면서 for문의 세번째 부분에 내용이 많아졌기 때문에 헷갈렸지만,
순서는 i++와 j++를 한 뒤, next[i]=j를 해줘야 한다는 것입니다. (next[i]=j부터 하면 안됩니다.)
그러면 아래와 같은 표를 다시 만들 수 있습니다.

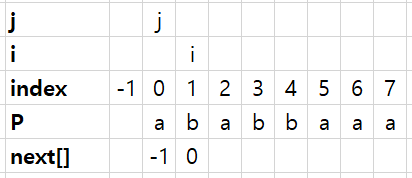
그리고 for문을 다시 살펴봅니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
현재 j=0이고 i=1이기 때문에 while()의 j >= 0 인 조건을 성립하고, p[i] != p[j]인 조건 또한 성립합니다.

p[0]!=p[1]이기 때문에 j=next[j]를 해줍니다.
j와 next[j]를 확인해 봅시다.

j=0이고 j에 next[0]의 값인 -1을 대입합니다.

while()을 검사했기 때문에, 다시 while()의 조건문을 확인해야 합니다. for문으로 가시면 안돼요.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
하지만 j=-1이기 때문에 while의 j >= 0 조건을 만족하지 않습니다.
따라서 while()을 나온 후 for(i = 0,j = -1; i < M; i++, j++, next[i] = j)로 돌아가서,
i++, j++, next[i]=j를 해주셔야 합니다.

next[i]=j를 할때는 주의해야할 점이, j를 찾아야 하는것이지 next[j]를 넣으면 안된다는 것.

그리고 다시 while()을 확인해줍니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
while(j >= 0 && p[i] != p[j]) 조건에서
j는 현재 0이기 때문에 while의 첫번째 조건인 j>=0을 만족합니다.
그리고 i는 현재 2이기 때문에
p[0]!=p[2]인 조건을 확인해야 합니다.
하지만 위의 표에서 보시다시피, p[0]은 'a'이고, p[2]도 'a'이기 때문에 p[0]!=p[2]인 조건을만족하지 않습니다.
따라서 while()문을 실행하지 않고 다시 for문으로 돌아갑니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
그리고 다시 i++,j++,next[i]=j를 해주셔야 합니다.

for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
그리고 다시 while(j >= 0 && p[i] != p[j])을 검사합니다.
현재 j는 1이기 때문에 while()의 j>=0조건을 만족합니다. 그리고 p[3]!=p[1] 조건을 확인하면, p[3]과 p[1]모두 'b'이기 때문에 해당 조건은 만족하지 않습니다.
따라서 for문으로 돌아간뒤 다시 i++,j++,next[i]=j를 해줍니다.

for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
그리고 다시 while(j >= 0 && p[i] != p[j])을 검사합니다.
현재 j는 2이기 때문에 while()의 j>=0조건을 만족합니다. 그리고 p[4]!=p[2] 조건을 확인하면, p[4]는 'b'이고 p[2]는 'a'이기 때문에 해당 조건을 만족하게 됩니다.
따라서 while()의 j=next[j]를 해줍니다.

그리고 다시 while()의 조건을 확인해줍니다.
현재 j는 0이기 때문에 j>=0의 조건을 만족합니다. 그리고 p[4]는 'b'이고 p[0]은 'a'이기 때문에 p[4]!=p[0]의 조건을 만족하므로 while()의 j=next[j]를 해줍니다.

그리고 다시 while()의 조건을 확인해줍니다.
현재 j는 -1이기 때문에 j>=0의 조건을 만족하지 않습니다. 따라서 while()을 빠져나간 뒤, for()로 돌아갑니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
while(j >= 0 && p[i] != p[j])
j = next[j];
그리고 i++,j++,next[i]=j를 해줍니다.
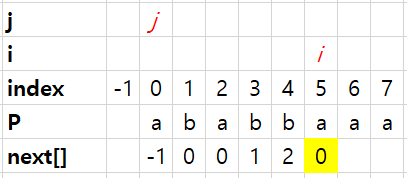
그리고 다시 while()의 조건을 확인합니다.
while(j >= 0 && p[i] != p[j])
j = next[j];
현재 j는 0이기 때문에 j>=0의 조건을 만족합니다. 하지만 p[5]는 'a'이고 p[0]도 'a'이기 때문에, p[5]!=p[0]의 조건을 만족하지 않습니다.
따라서 while()문을 들어가지 않고 다시 for()로 돌아갑니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
그리고 i++,j++,next[i]=j를 해줍니다.

그리고 while()의 조건을 확인합니다.
while(j >= 0 && p[i] != p[j])
j = next[j];
현재 j는 1이기 때문에 j>=0의 조건을 만족합니다. 그리고 p[6]는 'a'이고 p[1]이 'b'이기 때문에, p[6]!=p[1]의 조건을 만족하게 됩니다.
따라서 j=next[j]를 해줍니다.

그리고 다시 while()의 조건을 확인합니다.
while(j >= 0 && p[i] != p[j])
j = next[j];
현재 j는 0이기 때문에 j>=0의 조건을 만족하고, p[6]은 'a'이고 p[0]도 'a'이기 때문에 p[6] != p[0]의 조건을 만족하지 않습니다.
따라서 while()을 실행하지 않고 다시 for()문으로 돌아갑니다.
for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
그리고 i++,j++,next[i]=j를 해줍니다.

그리고 while()을 확인해줍니다.
while(j >= 0 && p[i] != p[j])
j = next[j];
현재 j는 1이기 때문에 j >= 0의 조건을 만족하고, p[7]는 'a'이고 p[1]은 'b'이기 때문에 p[7] != p[1]의 조건을 만족합니
다.
따라서

위와같이 변경됩니다.
그리고 다시한번 while()을 검사한다면 p[7]과 p[0]이 'a'로 같기 때문에 while()을 빠져나와서 다시 for()로 되돌아갑니다.
이때 i++,j++,next[i]=j 를 해주게 됩니다.

하지만 for문에서 for(i = 0,j = -1; i < M; i++, j++, next[i] = j)
i<M의 조건에 부합하지 않으므로 for문은 여기서 종료됩니다.
이렇게 표를 그려서 코드를 확인해볼 수 있습니다.
'--------------------**** > 알고리즘' 카테고리의 다른 글
| 다단계 합병에서 런의 분포 (0) | 2019.12.27 |
|---|---|
| 깊이 우선 순회 DFS - 스택 이용 (0) | 2019.12.26 |
| AVL 트리 설명 (0) | 2019.12.24 |
| KMP 알고리즘/개선된 KMP 알고리즘 & next[]의 FSM 다이어그램 (0) | 2019.12.21 |
| 알고리즘 공부했던 방법 (1) | 2019.12.14 |



